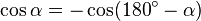Esta vez el supuesto es construir una mesa con las patas en aspa o en X. Con el libro excel calculo longitudes y cruces de las patas. Para el cálculo de unas patas en aspa, en principio, considero dos valores, la altura que queremos tener y la separación entre los extremos de las patas. Este supuesto es para patas simétricas. Las patas se cruzan en el centro del aspa. La parte carpintera permite, una vez fijadas la separación entre los extremos de las patas y ancho del listón, calcular el ángulo de corte y las distancias que indican por donde se cruzan ambas patas. Con la barra de desplazamiento de la hoja "Inicio" se selecciona el ángulo de corte (en décimas de grado) hasta alcanzar una la altura deseada.
Si queremos construir físicamente el aspa:
- Desde uno de los extremos trasportamos el ángulo con un transportador de ángulos, o llevamos la distancia aa' desde la esquina contraría siguiendo el listón.
- Llevamos las distintas medidas, según la gráfica de la hoja "Inicio"
Mi propia función en Excel:
- Los cálculos teóricos son básicamente trigonométricos.
- No son especialmente complejos, pero como llevo muchísimos años sin trabajar con senos, cosenos, tangentes, etc, me ha costado mas de la cuenta.
- Además, como he llegado a una función un poco demasiado compleja para mi perdida base matemática, decidí no intentar resolverla. Para mi era demasiado compleja y además quería resolverla de otra manera, con excel, tanteando con distintos valores hasta encontrar el valor mas aproximado posible.
- De paso toco de nuevo la posibilidad de hacer nuestras propias funciones con vbasic para excel.
- La función no resuelta es Altura=(DistEntrePatas-AnchoListón/SENO(RADIANES(a)))*TAN(RADIANES(a))
Este método solo funciona para funciones, o tramos de funciones, continuas y crecientes o decrecientes pero que no presenten ni picos ni valles. Las sucesivas aproximaciones se hacen fijando dos extremos, dos valores que sabemos que definen un tramo que cumple lo antes dicho, continuidad, crecimiento (o decrecimiento) y ausencia de picos y valles.
- Hay que calcular el ángulo que nos va a dar la altura deseada. Fijamos, por tanto, la la altura deseada, en este caso en la hoja Aprox F2, el ancho de tabla y la separación entre patas.
- Calculamos el valor medio de ambos extremos, en este caso el ángulo en grados.
- Calculamos, en este caso, las alturas en función de los grados, de los tres valores, límite inferior, límite superior y valor medio.
- Si la altura correspondiente al valor medio supera la altura deseada, el valor del límite superior pasa a ser el valor medio.
- Si la altura correspondiente al valor medio es inferior a la altura deseada, el límite inferior pasa a ser el valor medio.
- Si la función fuese decreciente el cambio de límites sería al contrario.
- Cada vez que se repite este proceso se aproximan los límites inferior y superior, hasta alcanzar el valor que resuelve nuestra ecuación.
- En el ejemplo hago 64 repeticiones, mas que suficientes para resolver mi irresoluta ecuación.
- Por otra parte, es poco práctico llenar una hoja de fórmulas bastante complejas cuando podemos crear una función en vbasic que nos resuelve nuestro problema.
- Con alt+f11 podemos ver los módulos con la programación vbasic del libro y ver las distintas funciones creadas para resolver la función que resuelve nuestro cálculo.
- En la hoja Aprox, celda L3 y columna E, utilizo un par de funciones creadas por mi. Su funcionamiento es idéntico a cualquier otra función propia de excel.